Height-Balanced BST

In this article, we are going to help you understand the general concept of a balanced BST.

What is a Height-Balanced BST?

Terminology used in trees:

• Depth of node - the number of edges from the tree's root node to the node

• Height of node - the number of edges on the longest path between that node and a leaf

• Height of Tree - the height of its root node

Aheight-balanced(orself-balancing) binary search tree is a binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. That is, the height of a balanced BST withN nodes is alwayslogN. Also, the height of the two subtrees of every node never differs by more than 1.

WhylogN?

• A binary tree with height

  h

  contains at most

  

  .

• In other word, a binary tree with

  N

  nodes and height

  h

  :

  

  .

• That is:

  

  .

Here is an example of a normal BST and a height-balanced BST:

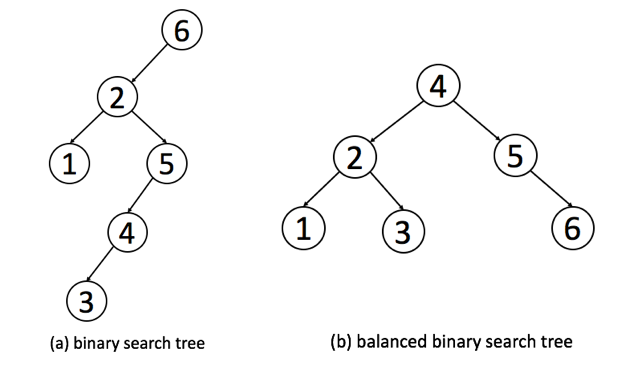
Using the definition, we can determine if a BST is height-balanced (Balanced Binary Tree).

As we mentioned before, the height of a balanced BST withN nodes is alwayslogN. We can calculate the total number of nodes and the height of the tree to determine if this BST is a height-balanced BST.

Also, in the definition, we mentioned a property of height-balanced BST: the depth of the two subtrees of every node never differ by more than 1. We can also validate the tree recursively according to this rule.

Why Using a Height-Balanced BST?

We have introduced binary search tree and related operations, including search, insertion and deletion in the previous article. When we analyze the time complexity of these operations, it is worth noting that the height of the tree is the most important factor. Taking search operation as an example, if the height of the BST is h, the time complexity will beO(h). The height of the BST really matters.

So let's discuss the relationship between the number of nodesN and the height of the treeh. For a height-balanced BST, as we discussed in the previous section,. But for a normal BST, in the worst case, it can degenerate into a chain.

Therefore, the height of a BST withN nodes can vary fromlogN toN. That is, the time complexity of search operation can vary fromlogN toN. It is a huge difference in the performance.

Therefore, a height-balanced BST play an important role in improving the performance.

How to Implement a Height-Balanced BST?

There are several different implementations for height-balanced BSTs. The details of these implementations are different but they have similar goals:

1. The data structure should satisfy the binary search property and the height-balanced property.

2. The data structure should support the basic operations of BST, including search, insertion and deletion within

   O(

   logN

   )

   time even in worst case.

We provide a list of popular height-balanced BSTs for your reference:

• Red-black tree

• AVL tree

• Splay tree

• Treap

We are not going to talk about the details of these implementations in this article series.

Practical Application of the Height-balanced BST

The height-balanced BST is widely used in practice since it can provide search, insertion and deletion operations all inO(logN)time complexity.

The most profound use is in set/map. The principle of set and map are similar. We will focus on the set in the following discussion.

Set is another data structure which can store a lot of keys without any particular order or any duplicate elements. The basic operations it should support are to insert new elements into the set and to check if an element is in the set or not.

Typically, there are two kinds of sets which are widely used:hash setandtree set.

Thetree set,TreeSetin Java orsetin C++, is implemented by the height-balanced BST. Therefore, the time complexity of search, insertion and deletion are allO(logN).

Thehash set,HashSetin Java orunordered_setin C++, is implemented by hash, but the height-balanced BST also plays an important role in hash set. When there are too many elements with the same hash key, it will cost O(N)time complexity to look up for a specific element, whereNis the number of elements with the same hash key. Typically, the height-balanced BST will be used here to improve the performance fromO(N)toO(logN).

The essential difference between the hash set and the tree set is that keys in the tree set areordered.

Conclusion

A height-balanced BST is a special form of BST which aims at improving the performance. The details of implementations are outside the scope of this article series and are not required in most interviews. But it is useful to understand the general idea of a height-balanced BST and how height-balanced BSTs can help you in your algorithm designs.